[转贴]美国斩杀线为什么刚好在1/e附近?
多个调查说明美国社会的斩杀线差不多是37%,也就是1/e附近。(搬运一个数据来源:美联储报告显示37%的美国人拿不出400美元应急现金。)
太诡异了,这背后是否必然存在一个用于描述的微分方程?
如果有,该是什么样的?为什么是1/e稳定?
我不敢信这仅仅是一个统计巧合。
这会是自发涌现的吗?
回答1:
没有任何管制的复杂系统,在极度追求效率和鲁棒性时,自然坍缩到的一个数学稳态。
所谓的1/e(约等于36.8%),在数学上最著名的应用是什么?
最优停止理论(Optimal Stopping Theory),俗称“秘书问题”或者“苏格拉底麦田问题”。
简单说:如果你要招一个秘书,想招到最好的,但你只能一个一个面试,面完就得决定录不录,不能回头。数学告诉你的最优策略是:无脑拒绝掉前37%(1/e)的人,把他们当作样本来建立标准,然后从后面的人里,选第一个比前面都强的人。
听懂了吗?
那37%的人,在数学上的定义就是——样本。
他们的存在意义,就是被系统观察和抛弃,用来给剩下的63%确立一个基准线!
把这个逻辑放到美国社会这个巨大的资本主义机器里,是不是瞬间就黑暗了起来?
那37%的底层(大概就是年薪几万刀以下,一旦失业立刻流落街头的群体),就是资本主义社会的耗材样本。
系统并不想把所有人都弄死,那样没人干活;系统也不想让所有人都过得好,那样劳动力成本太高,利润会归零。
假设 S 是社会的稳定度,P 是被剥削的程度(或者说贫困人口比例)。
恐惧驱动效率: 如果没人饿死,没人睡大街,那中间那60%的打工人就会变懒,会要求加薪,会罢工。所以必须有一部分人活在地狱里,作为活体广告展示给中间层看。这叫维持劳动纪律的必要代价。马克思管这叫产业后备军。
成本制约压榨: 如果饿死的人太多超过某个阈值,满大街都是丧尸,治安维护成本——警察、监狱、防弹玻璃就会指数级上升,甚至爆发革命,导致系统崩溃。
资本主义的算法,实际上是在求解一个泛函极值: 如何在最小化维稳成本的同时,最大化打工人的恐惧感(即劳动效率)?
在这个方程里,那个37%,就是系统鲁棒性的临界点。
这很像信息论里的熵。函数 -x \ln x 的极值点在哪里?就在 1/e 附近。 这说明什么?说明维持37%的人处于“薛定谔的死活状态”——既在这个社会里活着,又好像已经死了;既是劳动力,又是废料——这种状态下,系统能榨取的信息量,或者说从混乱中提取的秩序是最大的。
为什么是1/e稳定?
因为如果这个比例小于37%,比如只有10%的人穷,那剩下90%的人会觉得自己很安全,他们会联合起来对抗资本,资本的利润率会下降。
如果这个比例大于37%,比如50%的人都活不下去了,那社会的混乱程度(熵)会超过警察系统的控制能力,富人的资产安全就没有保障。
只有在1/e这个位置:
足够多的人在受苦,多到让你下楼买咖啡时不得不跨过流浪汉的身体,让你时刻在这个巨大的“样本库”面前瑟瑟发抖,不敢迟到早退。
足够多的人还能勉强维持生活(那63%),他们虽然也是牛马,但看到那37%的惨状,会产生一种虚幻的“优越感”和“幸存者偏差”,从而拥护这个系统,甚至会去嘲笑那37%不够努力。
他们就像挂在城门上的头颅,时刻提醒着剩下那63%的中产和准中产:看见了吗?你要是不努力996,不接受降薪,那就是你的下场。
并没有一帮共济会的大佬坐在圆桌前说“我们要把贫困线定在1/e”。
而是无数个公司、无数次裁员、无数个法案、无数次警察出警,在长达百年的博弈中,自动进化到了这个最经济、最“耐操”的比例。
任何偏离这个比例的尝试,都会被市场这只“看不见的手”给修正回来:
福利发多了,通胀就把底层打回原形。
压榨太狠了,零元购和骚乱就会逼着政府发点粮票。
最终,社会就像一个被设定好程序的各种物理粒子,自动停在了能量最低、结构最稳定的坑里。而这个坑的深度,恰好就是自然对数的底。
这才是最恐怖的。
如果是因为有人坏,那你还可以把坏人挂路灯。
但如果这是数学规律,是私有制+自由市场+极度异化后的必然数学收敛……
那你面对的不是一个暴君,而是一个冰冷的、不可违抗的物理定律。那37%的人,不是不幸,他们是这个方程里必须被牺牲掉的那个分母,为了让分子显得更有意义。
这就是现实中的完美的资本主义地狱:这里没有鬼神,只有精准得令人作呕的算术。
回答2:
因为e分之1就是所谓的“倒霉常数”。
就好像你在游戏里抽卡,百分之一出货率下你抽一百次没出货,你会认为是自己倒霉;万分之一出货率下你抽一万次没出货,你也会认为自己倒霉。
你用计算器按一下这两者的几率就会发现很接近(四舍五入均为约37%)。那么你继续带入一百万、一亿、一百亿。。。就会发现几率无限逼近e分之一。
没错,e分之一就是(1-1/n)^n的极限。
这就是随机系统自发的趋势:当成功几率和机会次数互为倒数时,约有37%的人会倒霉。
政府不有意管人民也不故意害人民时,这就是自然的常数,这就是天理。
现在你可能想问:那么咱们有没有办法不让那么多人倒霉啊?
当然有。
不让成功几率和机会次数互为倒数就可以了。机会的次数是成功率倒数的2倍,倒霉的人就只有13%了;提高到3倍,倒霉的人就只有不到5%了;提高到4倍,倒霉的人就不到2%了;提高到5倍,倒霉的人就不到1%了。
在你倒霉(用完天经地义的机会次数之后还没能成功维持生存)时多给你几次机会——这就是我国政府在做的事。
而在你倒霉(用完天经地义的机会次数之后还没能成功维持生存)时直接结束游戏——这就是美国政府做的事,也就是所谓的斩杀线。
天理就规定了37%的人要倒霉,而我们的政府就是为了人民在逆天而行。
回答3:
其实是一个非常经典的问题,在quant求职时常见的brain teaser,而且只需要基本的高等数学知识即可完成。
这个问题的基础版本包括但不限于:假设十年时间里每年都不重复地谈一次恋爱,那么选择在第几次结婚?
去麦田摘麦穗,假设每棵麦穗只能经过一次,怎么找出最大的麦穗?
这类问题都有一个共同点,即:给定数量的样本范围,在每个样本只有一次观察的机会(即要么选择要么放弃)的前提下,如何操作,使得找出最优样本的概率最大?
这里找出最优解需要考虑三个点,首先,我们希望考察这个样本集合的大致水平,以便尽可能估计最优样本的水平,为实现这个目的,需要预先观察若干个样本,观察后再进行选择;其次,对每个样本,观察机会只有一次,自然希望最优解没有出现在预先观察的样本集合中;最后,在完成对样本的预先观察后,只要新观察的样本比预先观察集合中的局部最优样本更好,就视为全部样本中的最优解,结束观察,那么自然希望次优解出现在预先观察的样本集合中,并假设次优解出现在最优解之前。
明确了这三点,就可以开始解决这个问题了,问题求解如下:
样本集合为 \left\{ X_{i} \right\}(1\leq i\leq n) ,预先观察的样本集合为 {X_{i}}(1\leq i \leq k) ,记
X_{j}=max{X_{i}} (1\leq i \leq n) , X_{l}=X_{(n-1)} ,观察k个样本后找出最优样本的概率为 P_{k} .
由前述第二个点, k
这个图像眼熟了一些吗?
是不是很接近自然界的各种螺线?
大自然的对数螺旋
在几种自然现象中,你会发现几乎是对数螺旋的曲线。比如:
鹰找到猎物:他们最清晰的视野与他们的飞行方向有一定的角度。这个角度与对数螺旋的夹角相同。
昆虫到光源:它们习惯于将光源与飞行路径保持恒定角度。通常,太阳(或夜间物种的月亮)是唯一的光源,以这种方式飞行将导致几乎直线。 但是人造光源离得太近,虽然它们夹角恒定,但是会导致越飞越近造成飞蛾扑火的现象。
螺旋星系的臂。我们的银河系,有几个螺旋臂,每个螺旋都大致是一个对数螺旋,螺距约为12度。

角膜神经 (这是几种不同动物的角膜神经,以对螺旋模式在角膜的浅表皮层附近终止)。
热带气旋,例如飓风。
许多生物结构,包括软体动物的壳。
由此可见e在自然界存在非常广泛,但是这还不是它叫做自然底数的原因。
e是这样定义的:
当n趋近于无穷大时,(1 + 1/n)^n的极限,即e = lim_{n→∞} (1 + 1/n)^n
它之所以叫自然底数,源自它那古希腊哲学一般的形式美感:e 的一个重要性质是它是唯一一个使得其导数等于自身的数。也就是说:
函数 f(x)= e^x的导数 f′(x)也等于 e^x
这使得它在微积分和数学分析中非常重要。
简单来说,我们可以认为e的本质是连续不断的增长(或衰减)。
现实世界中,极少有事情是像光电效应一样到一定数值才激发,大多数事情(细菌分裂、谣言传播、资产增值)是每分每秒都在发生的。所以用到e的地方会很多。
比如假设你有 1 块钱,银行很大方,年利率 100%。
一年结一次息: 年末你有 2 块钱。
半年结一次息,到了年底你就有 :
(1+1/2)2=2.25(1+1/2)2=2.25
每天结一次息,到了年底你就有 :
(1+1/365)365≈2.714(1+1/365)365≈2.714
要是银行用电脑给你每秒、每毫秒、连续不断地结息呢?
那到了年底你就有 \lim_{n \to \infty} (1 + \frac{1}{n})^n = e \approx 2.71828…
这就是这就是连续复利公式的由来 :
A = P ⋅ e ^r t
它告诉我们,靠“利滚利”的频率来增加财富是有天花板的。
你在一年的时间里不能通过无限次地结算利息来把 1 块钱变成 100 万,宇宙的极限锁死在了 2.718 倍左右(在 100% 利率下)。
那么,复利增长可以用e,价值衰减能不能用e呢?
也是可以的。
我经常在网上买二手的东西电子产品,会发现一个有趣的现象。
所有新的电子产品,只要拆开激活使用就开始贬值,不管你是用一次还是十几次,都会跌一个让你肉疼的价格,大几千的新机器,使用几次后不是你降价几十或者100块钱就能卖出去的,比如我买了一个12月1日才激活仅使用过一次的无人机,原价1500,卖家最终1200出售。
大多数电子商品使用一年左右,价格会跌到原价的一半以上。
但是你这个时候买二手的再用两个月,价格不会变成原价的1/4,而是依然能以差不多始发价半价卖出去。
其实仔细算算并非一半,而是接近36.8%,也就是e的倒数1/e。
举个例子,你今天买了一个一万的新苹果手机,但是你打开激活的一瞬间就开始贬值了。
你支付的购置税、保修、新手机溢价等费用,在转手时没人会考虑。
这部分贬值是即时且剧烈的,通常在第一个月就能损失原价的 10% 到 20% 甚至更高。
也就是说不管你是开了一周还是一个月,要卖的话估计都要有10%左右的跌价损耗。
过了这个剧烈衰减期间,后面价格的变化就按照指数衰减:
V(t) = V_0 \cdot e^{-kt}
V指的是商品的初始价值(比如新车的购买价)。
k衰减率常数。这个值越大,商品贬值越快。
这个公式意味着你买的商品的价值不是固定数量的减少,也不是固定百分比的减少(比如每年都减少几千块钱),而是每单位时间减少一个固定百分比。而正是这种“连续复利式”衰减的数学基础。
假如我们取k=1,单位时间一年,也取做1。
那么我们的苹果手机一年后会贬值到原价格的1/e,就约等于36.8%
当然,现实生活中苹果贬值没这么快,这里单位时间要久一点。
我这里找了一个我2021年买的苹果12:
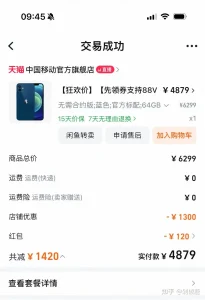
当时的价格是4879,如果我现在放到二手平台能卖多少呢?
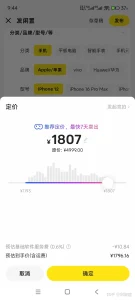
最近的最高成交价是1807左右(且品相完美),意味着高于这个价格可能就很难卖出了。
那么这个价格就是1807/4879≈37%
看,我们的37%出现了!
很有趣是吧。
只要增长或者衰减是连续的,我们总是很容易的能找到e能见缝插针的地方。
所以回到我们的斩杀线上。
37%的概率恰恰是数学上的最优停止理论。
这其实跟苏格拉底捡麦穗是一样的概率。
相传,苏格拉底的三个弟子曾向他请教如何找到最理想的伴侣。
苏格拉底并未直接回答,而是让他们走进一片麦田,要求他们分别从中选择一支最大的麦穗,且只能摘一次,不能回头。
第一个弟子刚走几步就摘了一支自认为最大的麦穗,但后来发现后面还有更大的,于是遗憾不已;
第二个弟子则一路犹豫不决,最终空手而归;
第三个弟子则吸取前两人的教训,他先观察麦穗的大小,分出大、中、小三类,然后在最后三分之一的路程中果断选择了比参照物更大的麦穗,最终满意而归。
假设一共有N个麦穗(可以预见,N这个数字很大)如果你随机选,选中的概率是 1/N
如果你把所有麦穗都看完,你只能选最后一个,但它未必是最大的。
数学家的策略(37%法则):
你应该把前 37%(准确地说是 1/e)的数据作为“观察样本”。
对这前 37% 的麦穗,无论多大,统统不要,但记下它们中最大的一个X
从第 37% 个麦穗之后开始,一旦遇到一个比X大的麦穗,立即采下来,能确保你采的麦穗在策略上是最大的。
数学证明,使用这个策略,你选中最大麦穗的概率,竟然也刚好是 37%(准确地说是 1/e)左右。
这说明37%就是在不确定性面前,人类能达到的数学极限。
也就是说,斩杀线37%可能确实是巧合,但是如果我们真打算淘汰一些人,留下那些比较好,那么淘汰最底下的37%可能就是社会达尔文丛林里给出的终极答案了。
抽卡也是同样的道理,当样本量足够大(趋向于无穷大)时,如果你有 1/n的概率中奖,尝试 n次,你一次都中不了的概率,就是 1/e,也就是 36.8%左右。
也就是说1/100的抽中概率,你抽100次一次也不中的概率居然高达36.8%,正因为如此,游戏厂商才要设置保底,免得你卸载游戏。
自然底数e就是这么神奇啊~